Jingkun (Allen) Liu

Current Master of Science in Robotics student at Northwestern University, with expertise in ROS/ROS2, C/C++, and Python. Passionate about Robotics, Embedded Systems, Automation, Control, and Human-Computer Interaction.

Jack and Box Simulation

Python, SymPy, Dynamics

Authors: Allen Liu

GitHub: View this Project on GitHub

Project Description

Used Jupyter notebook to perform the calculation about physics model of a jack with a box with some force applied upon the box.

Structure

Rigit Body Transformation

To model the dynamics about the jack and the box, we defined all necessary frames as shown in figure below:

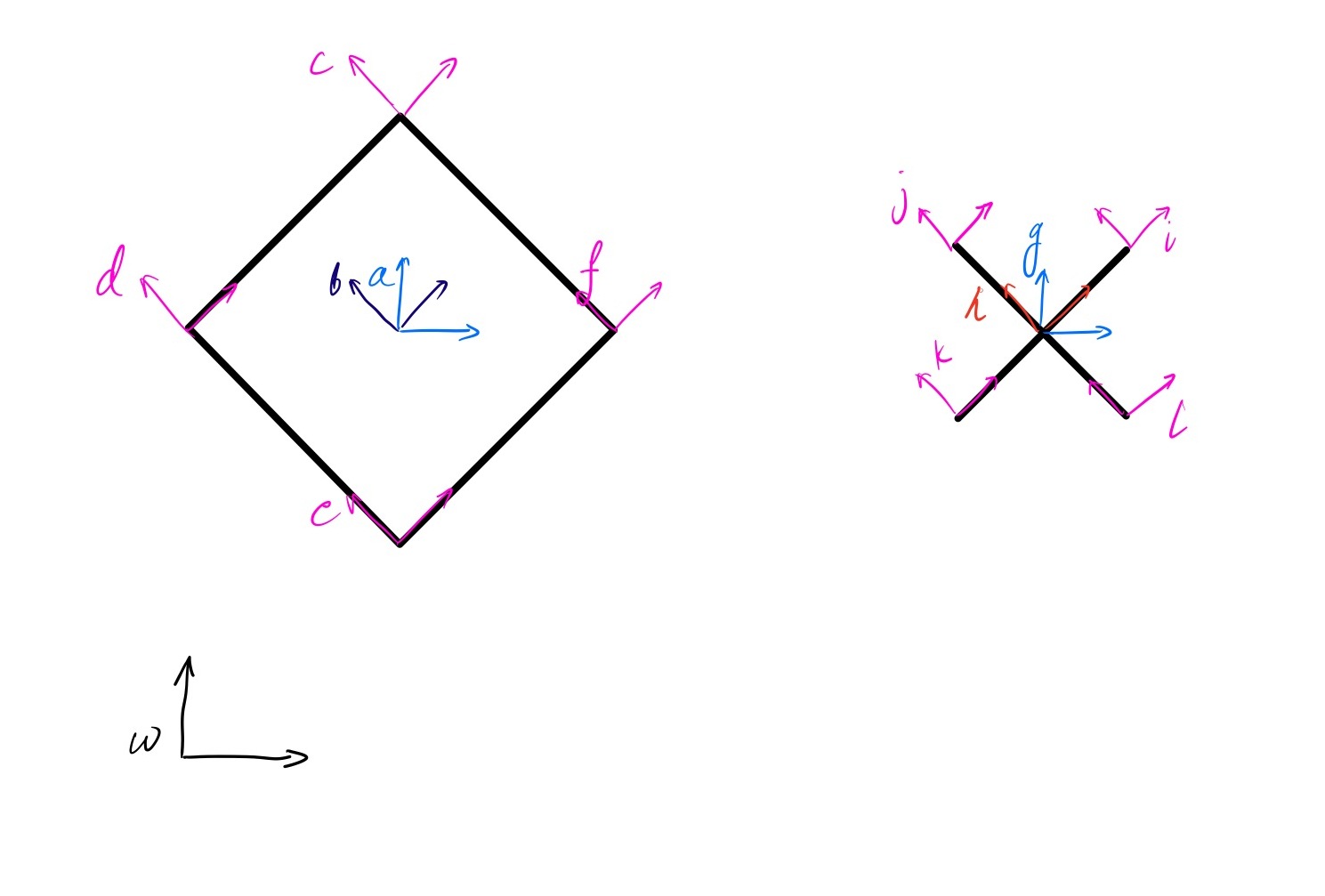
Then we can calculate the transformation between all frames:

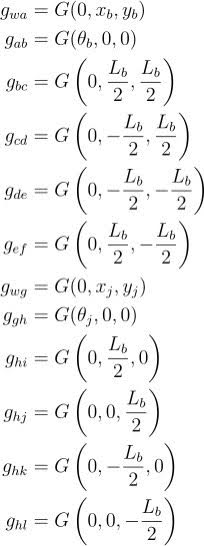
Euler-Language Equation Formulation

In this project, to simplify the problem, we model the jack as 4 point mass with same mass, m_j, and model the box with the mass m_b and moment of intertia of I_b, so that the total kinetic energy and potential energy can be easily obtained by this

Impacts

Amination

12 Dec 2023

« Polyglot Translator Robot Fixing Rethink Sawyer Robot Arm »

Explore →

iOS Application Development (1) Firebase (1) Firestore (1) Storage (1) Cloud Function (1) CRUD (1) Swift (1) Storyboard (1) Python (7) Wavefront (1) Recursive Backtracking (1) Randomized Prim (1) RRT (1) OpenCV (2) ROS2 (4) MoveIt2 (2) Interbotix Pincher PX100 (1) MATLAB (1) Robot Dynamics (1) Feedback Control (1) Feedforward Control (1) Mobile Manipulator (1) CoppeliaSim (1) OCR (1) YOLO (2) Emika Franka Robot Arm (1) SymPy (1) Dynamics (1) CMOS (1) Rethink Sawyer Robot Arm (2) Intra OS (1) Embedded Linux (1) Robot Hardware (1) SLAM (1) EKF (1) C++ (3) Open Robotics Turtlebot3 Burger (1) 2D LiDar (1) ROS1 (1) Linux (1) Bash Shell (1) MoveIt! (1) Navigation (1) Interbotix PincherX-100 Robot Arm (1) Clearpath Ridgeback Mobile Platform (1) React (1) Java (1) SpringBoot (1) MySQL (1) UART (1) ATMega2560 (1)