Turtlebot3 Navigation Using Deep Reinforcement Learning
C++, ROS2, Open Robotics Turtlebot3 Burger, 2D LiDar, OpenAI Gymnasium, Deep Reinforcement Learning
Description
In this project, I designed and implemeted a OpenAI gymnasium environment for training a model for controlling the turtlebot3 to navigate through a hallway.
Demo Video
The result of this project cam be shown in the video below:
Odometry Model
For this project, since the focus is the control of a turtlebot3, not localization, so I assume the perfect odometry for this project.
To get the odometry from the wheel angle and velocity, it applied kinematics model from Modern Robotics to conduct the Forward Kinematics and Inverse Kinematics of the robot.
The geometry model of the robot can be present using $H$ matrix.
\[\begin{align*} H(\theta) &= \begin{bmatrix} h_1(\theta) \\ h_2(\theta) \end{bmatrix} \\ h_i(\theta) &= \frac{1}{r_i \cos{\gamma_i}} \begin{bmatrix} x_i \sin{\left (\beta_i + \gamma_i \right )} - y_i \cos{\left (\beta_i + \gamma_i \right)} \\ \cos{\left ( \beta_i + \gamma_i + \theta \right )} \\ \sin{\left ( \beta_i + \gamma_i + \theta \right )} \end{bmatrix}^\intercal \end{align*}\]For the Turtlebot3, which is a diff-drive mobile robot. The parameters are defined as
So that \(H(0)\) can be calculated as
\[H(0)=\begin{bmatrix} -d & 1 & -\infty \\ d & 1 & -\infty \end{bmatrix}\]Where \(d\) is the one-half of the distance between the wheels and the \(r\) is the radius of the wheel.
Hence \(F\) matrix can be calculated by
\[F=H(0)^\dagger = r \begin{bmatrix} -\frac{1}{2d} & \frac{1}{2d} \\ \frac{1}{2} & \frac{1}{2} \\ 0 & 0 \end{bmatrix}\]Forward Kinematics
The forward kinematics is to find the tranform from current state to next state \(T_{bb'}\) given the change in wheel positions \(\left( \Delta\phi_l, \Delta\phi_r\right)\).
- Find the body twist \({\cal V}_b\) from the body frame of the current state to next state:
- Construct the 3d twist by
- Then, the transform from current state to next state \(T_{bb'}\) can be calculated by
Inverse Kinematics
Inverse kinematics is to find the wheel velocities \(\left(\dot{\phi_l}, \dot{\phi_r} \right)\) given the body twist \({\cal V}_b\).
The wheel velocities can be calculated as
\[\begin{bmatrix} \dot{\phi}_l \\ \dot{\phi}_r \end{bmatrix} = H(0){\cal V}_b = \frac{1}{r}\begin{bmatrix} -d & 1 & -\infty \\ d & 1 & -\infty \end{bmatrix} \begin{bmatrix} \omega_z \\ v_x \\ v_y \end{bmatrix}\]Since this robot is non-holonomic so that it cannot move sideways. Hence \(v_y=0\), then the wheel velocities \(\left(\dot{\phi_l}, \dot{\phi_r} \right)\) are:
\[\begin{align*} \dot{\phi}_l &= \frac{1}{r} \left ( -d \omega_z + v_x\right) \\ \dot{\phi}_r &= \frac{1}{r} \left ( d \omega_z + v_x\right) \\ \end{align*}\]OpenAI Gymnasium
To start the training pipeline of the turtlebot3, I wrapped the ROS2 turtlebot3 simulation within the OpenAI gymnasium environment.
Observation Space
The observation space for the environment can be defined as
\[\begin{align*} x &= -1 \rightarrow 4 \\ y &= -0.5 \rightarrow 4.5 \\ \theta &= -\pi \rightarrow \pi \end{align*}\]Action Space
The action space can be defined as
\[\begin{align*} \dot{x} &= 0.0 \rightarrow 0.2 \\ \dot{\theta} &= -0.5 \rightarrow 0.5 \end{align*}\]Reward
The reward is defined as -1 when it hits a wall and 1 when it reaches the goal.
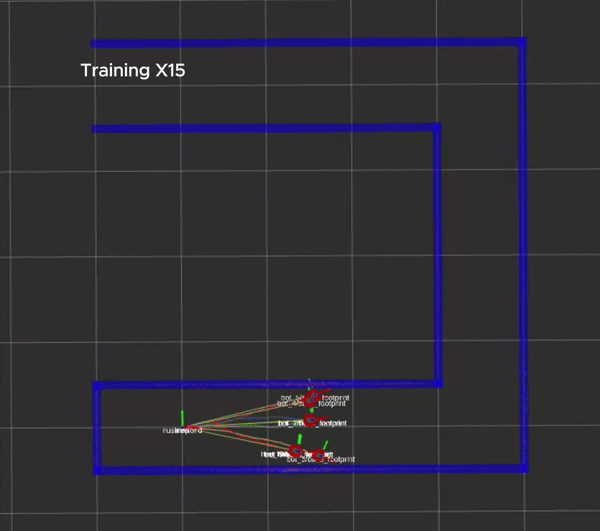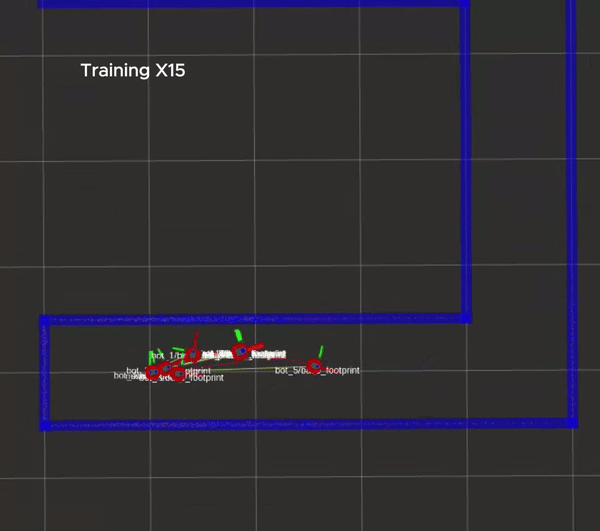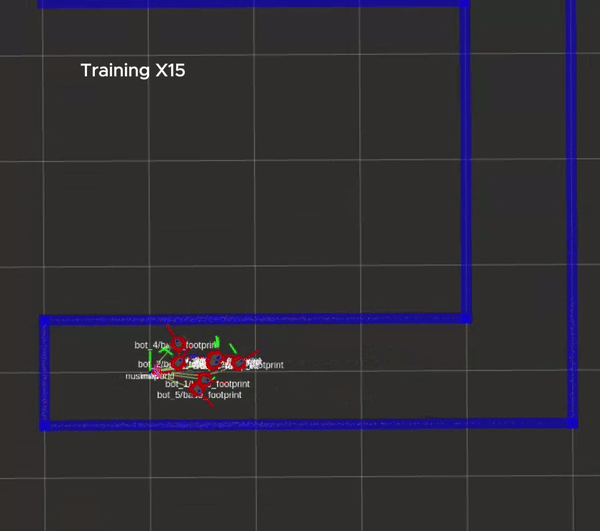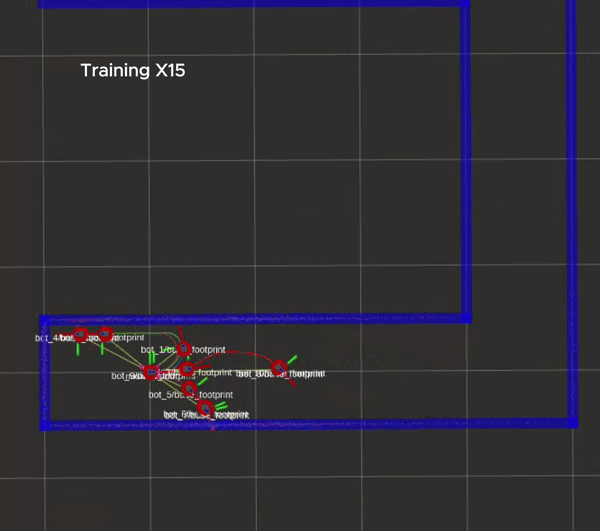
Traning
The training process is shown in the figure below, in which every robot will be reset to its original position whenever it hits a wall.
Packages
nuturtle_description: Visualizing the pose of the turtlebot3 burgerturtlelib: Call customized library functions for kinematics and slam calculations.nusim: Simulate the turtlebot in the real world.nuturtle_control: Performing the turtlebot kinematics calculation and parsing the command sent to theturtlebot3.nuslam: Performs the SLAM algorithm for correcting the error odometry.nuturtle_interfaces: All message interfaces for communication between the nodesnuturtle_slam: Integrateslam_toolboxfor setting up learning environmentnuturtle_deeprl: Wrapped withOpenAI Gymnasiumfor Deep Reinforcement Learning traing environment