AI-Powered Autunomous Tangram Puzzle Solver
C++, Python, ROS2, YOLO, Convolutional Autoencoder, Sematic Segmentation, Computer Vision, Machine Learning, Robot Kinematics
Source Code: The source code for this project can be found here: GitHub
Objective
The objective of this project is to design and implement a robotic system capable of solving tangram puzzles specified by the user. Tangram puzzles are NP-hard problems, presenting a significant challenge for robotic systems to solve. This project aims to develop a system that integrates advanced algorithms to sense, plan, and control a robotic arm, enabling it to accurately assemble tangram pieces to match the target puzzle configuration. By leveraging cutting-edge technologies such as computer vision, machine learning, artificial intelligence, and robotic manipulation, this project seeks to demonstrate the capability of robotic systems to perform complex tasks with precision and efficiency.
Hardware Setup
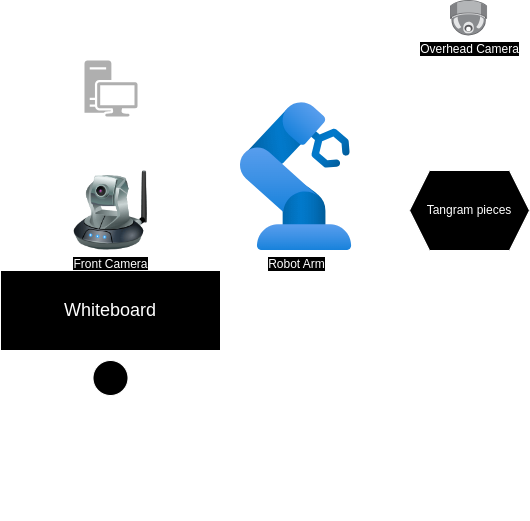
The hardware setup is shown in the picture below. This system consists of a robot arm and two cameras, which includes one overhead camera and one :
- Robot Arm: To manipulate the tangram pieces to solve the tangram puzzle.
- Overhead Camera: To detect the poses of tangram pieces.
- Front Camera: To detect the outline of the puzzle to solve.
Hand-Eye Calibration
The setup for performing hand-eye calibration involves placing an AprilTag within the workspace of the robot arm, as shown in the figure below. The calibration mechanism aligns the robot arm’s end-effector with the AprilTag. By calculating the homogeneous transformation, the transformation between the robot frame and the camera frame can be determined.
Denoting $ r $ as the robot frame, $ c $ as the camera frame, and $ t $ as the tag frame, the transformation $ T_{rc} $ between the robot and camera frames can be calculated using the relationship:
\[\begin{aligned} T_{rc} &= T_{rt} \cdot T_{tc} \\ &= T_{rt} \cdot T_{ct}^{-1} \end{aligned}\]Here:
- $ T_{rt} $: Transformation from the robot frame to the tag frame.
- $ T_{tc} $: Transformation from the tag frame to the camera frame.
This method ensures accurate calibration of the system, enabling precise spatial localization and coordination between the robot arm and the camera.
System Workflow
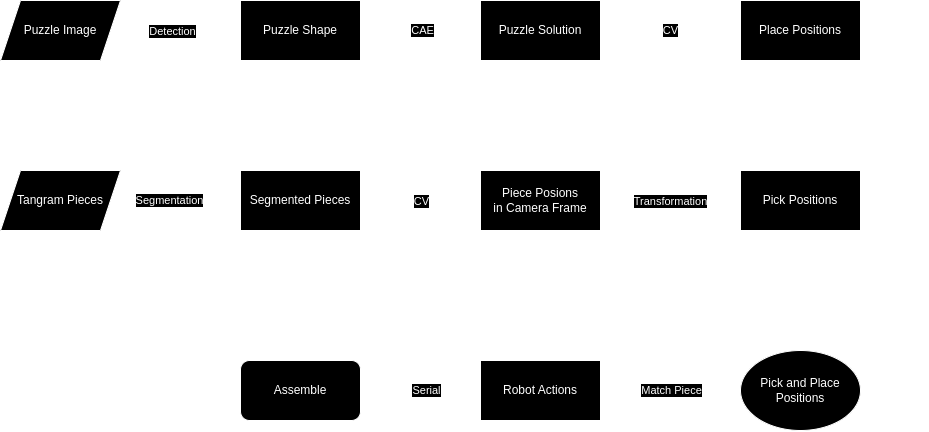
Software Architecture
Tangram Puzzle Detection
For puzzle detection, I trained a YOLOv11 object detection model to identify shapes drawn on a whiteboard. Once a shape is detected, the system retrieves the corresponding image from the database. The selected shape image is then fed into the tangram puzzle-solving model for further processing and solution generation.
Tangram Puzzle Solver
To tackle the challenge of solving tangram puzzles, I leveraged insights from the paper Generative Approaches for Solving Tangram Puzzles. The paper introduces a solution using a Convolutional Autoencoder (CAE) specifically designed for tangram puzzle segmentation.
The CAE system processes the tangram puzzle as its input and generates segmented shapes as its output, enabling a step-by-step solution to the puzzle. The figure below illustrates the input-output relationship, showcasing the CAE’s capability to effectively decompose the puzzle into its constituent shapes.

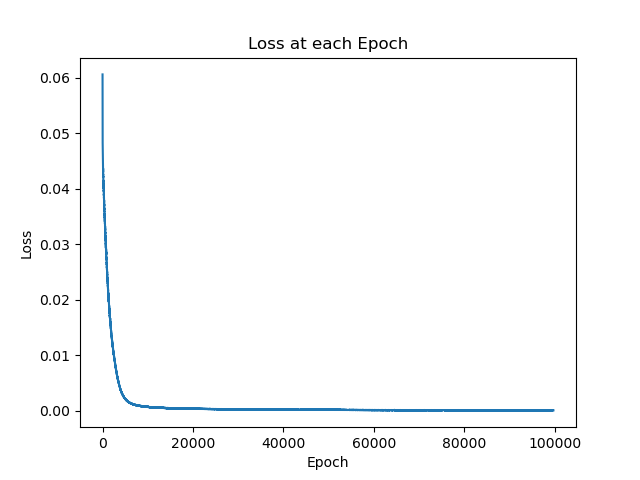
The training loss over epochs is depicted in the figure below, demonstrating the model’s convergence during training:
Target Pose Detection
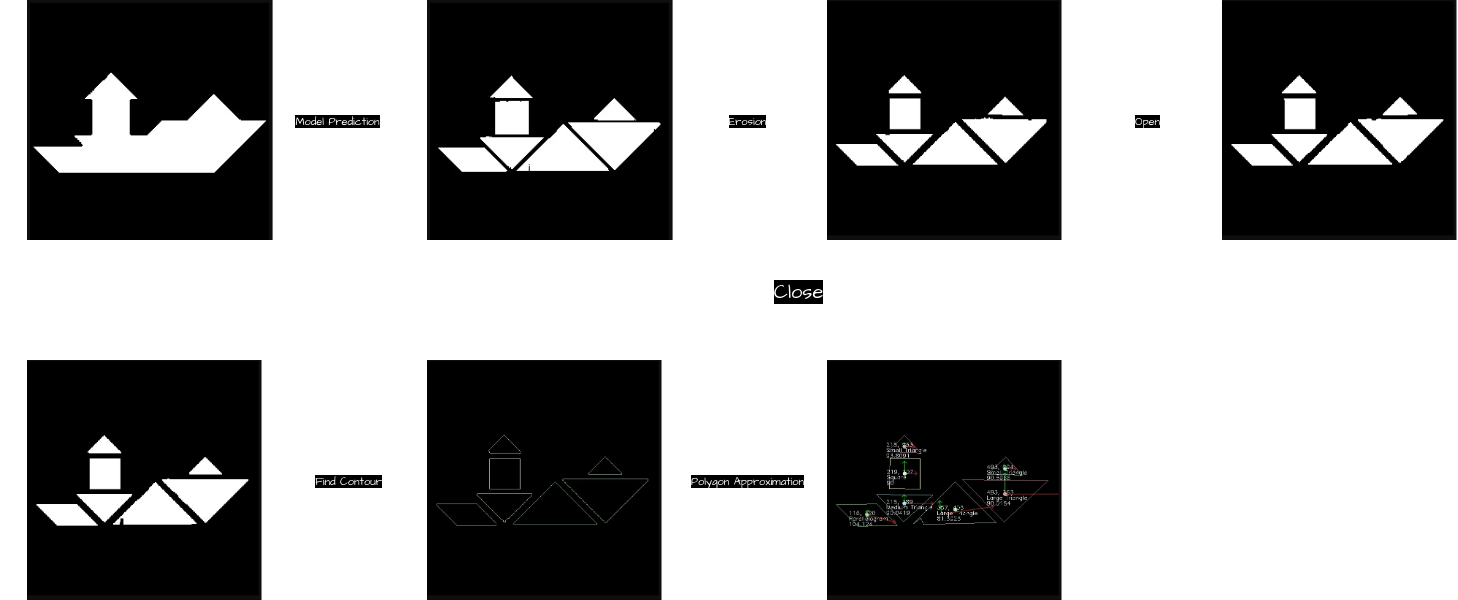
The process to determine the configuration of each tangram piece in the robot frame is outlined in the diagram above. This workflow ensures accurate identification and localization of each tangram piece, enabling effective robotic manipulation. The process is divided into the following steps:
- Model Prediction (CAE): The puzzle image is processed using a trained Convolutional Autoencoder (CAE) to segment the tangram puzzle into individual pieces and identify their target configurations.
- Erosion: The boundaries of each segmented mask are eroded to prevent adjacent tangram pieces from being erroneously connected.
- Opening: Morphological opening is applied to remove white noise from the black background, ensuring clean segmentation of the puzzle pieces.
- Closing: Morphological closing is used to eliminate black noise within the tangram pieces, preserving their integrity.
- Find Contour: The
Cannyedge-detection algorithm is employed to locate the contours of each tangram piece, isolating their edges. - Approximate Polygon: The detected contours are approximated to the closest polygon, enabling precise determination of each tangram piece’s shape and orientation.
This comprehensive approach leverages the CAE model and robust image processing techniques to ensure tangram pieces are accurately configured within the robot’s frame, facilitating precise and efficient robotic operations.
Tangram Piece Detection
To enable the robot arm to accurately pick up tangram pieces, I implemented semantic segmentation combined with morphological transformations. This approach effectively identifies the shape and pose of each tangram piece, ensuring precise localization for robotic manipulation.
Tangram Pose Detection
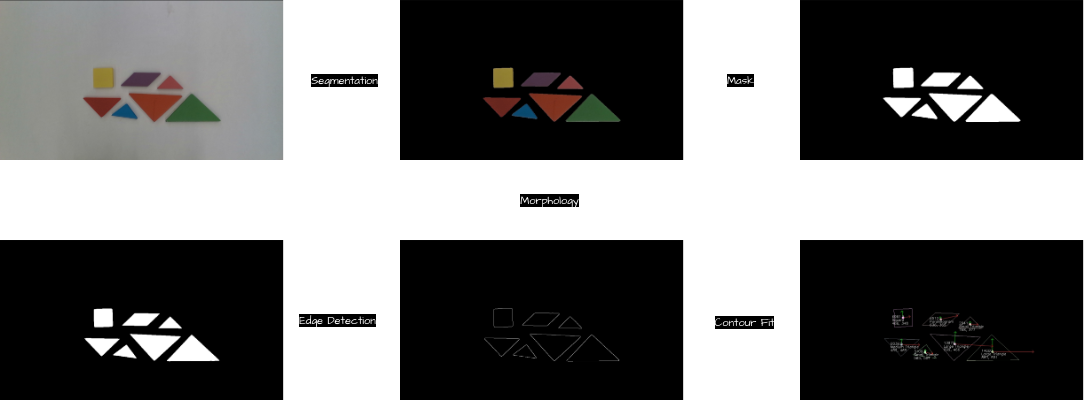
As illustrated in the figure above, the workflow for detecting the pose of tangram pieces includes the following steps:
- Semantic Segmentation: Segment the input image to identify individual tangram pieces.
- Mask Generation: Generate a mask from the segmented image to isolate each tangram piece.
- Edge Detection: Apply edge-detection algorithms to identify the contours of the tangram pieces from the masked image.
- Contour Analysis: Analyze each detected contour to determine its centroid, shape, and orientation.
- Deprojection: Transform the $ x, y $ pixel coordinates into $ x, y, z $ Cartesian coordinates within the camera frame, enabling precise 3D localization of the tangram pieces.
Frame Transformation
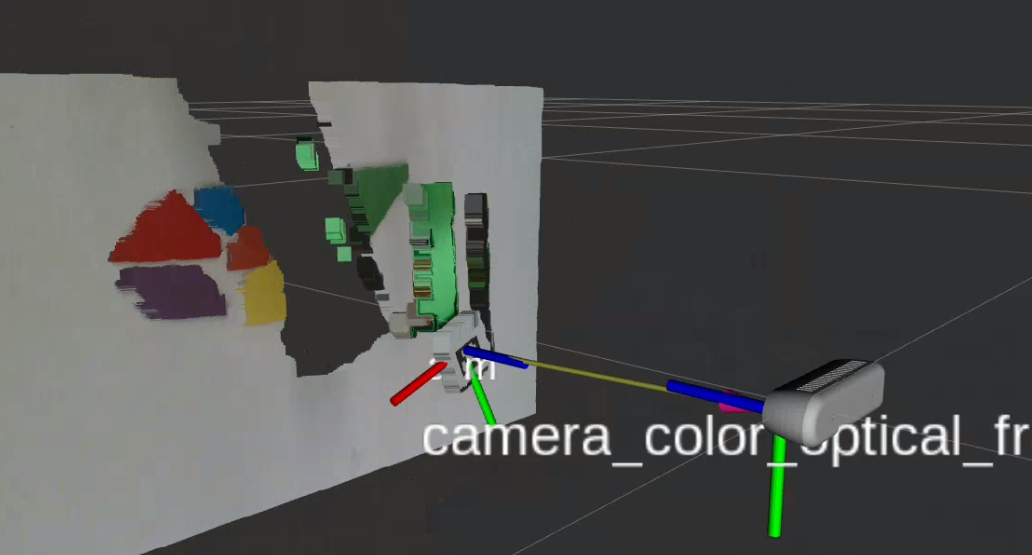
From the Hand-eye Calibration step, the transformation matrix $ T_{rc} $ (robot frame to camera frame) was obtained. Using this transformation, the position of each tangram piece in the camera frame ($ \vec{p}_c $) can be converted to the corresponding position in the robot frame ($ \vec{p}_r $).
The transformation is computed as follows:
\[\vec{p}_r = T_{rc} \times \vec{p}_c\]This calculation enables accurate localization of tangram pieces in the robot’s coordinate frame, ensuring precise robotic manipulation during the assembly process.
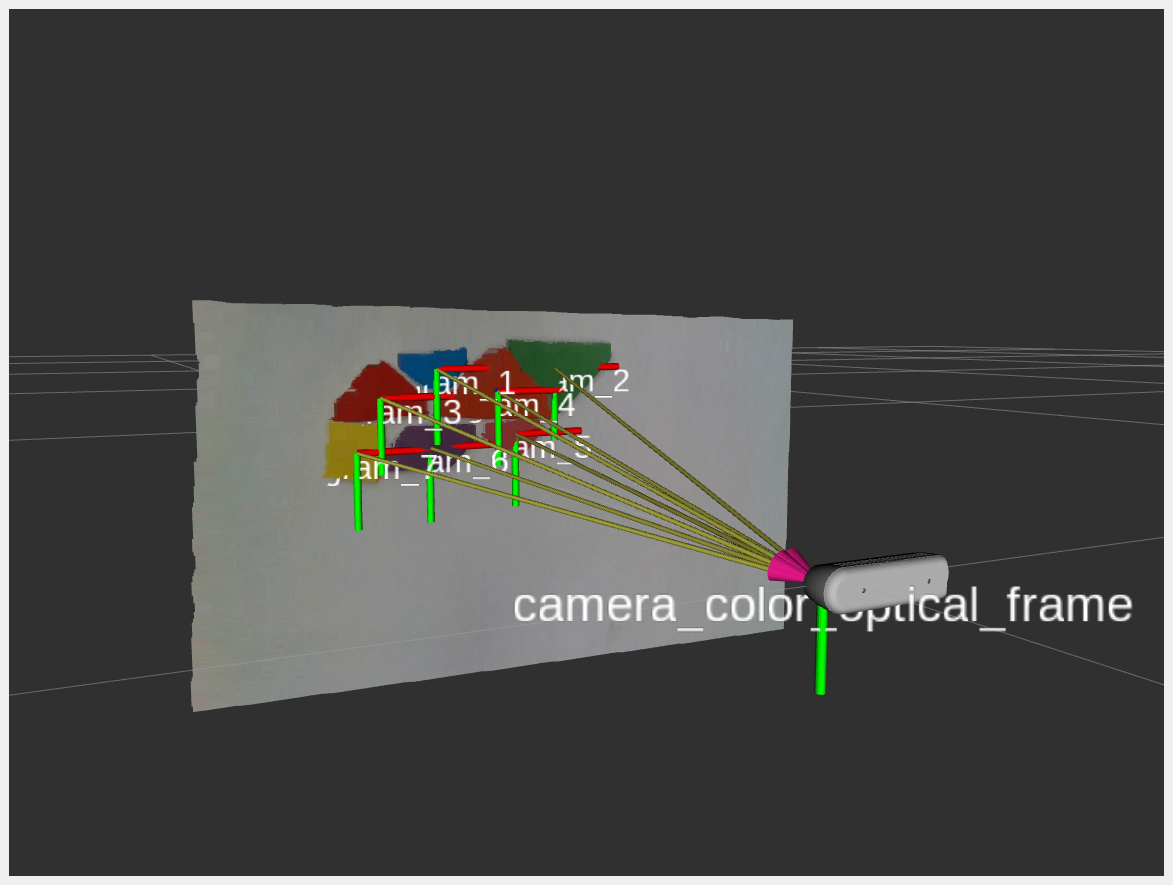
The resulting detected position of each tangram piece in the camera frame is shown in the figure below:
Robot Action Planner
Once the poses of the tangram pieces and their corresponding target positions were determined, I developed a detailed sequence of robotic actions to facilitate the assembly process.
The workflow involved the following steps:
- Pose Mapping: Using the computed current and target poses, the system calculated the optimal path for each piece.
- Pick-and-Place Strategy: The robot arm was programmed to execute precise pick-and-place actions. This involved:
- Moving to the detected position of each tangram piece.
- Adjusting the gripper for secure grasping based on the shape and orientation of the piece.
- Lifting the piece without disturbing adjacent ones.
- Path Planning: Trajectories were generated to ensure smooth and collision-free motion from the current pose to the target pose.
- Placement Accuracy: At the target position, the robot arm adjusted the piece’s orientation to match the desired alignment and gently placed it into position.
This process enabled the robot to systematically pick up each tangram piece and assemble them into a complete puzzle with high precision and efficiency.
Robot Controller
The robot arm, powered by four servo motors, is operated through precise angle adjustments for each motor. To enable accurate movement to specified x, y, z Cartesian coordinates, I implemented forward and inverse kinematics. This ensured precise motion control and positioning of the robot arm within the Cartesian space.
Kinematics
To develop the forward and inverse kinematics for the robotic arm, I referred to the textbook Modern Robotics. Using this resource, I modeled and implemented the kinematics algorithms required for precise control of the robot arm’s motion.
Robot Modeling
As shown in the figure below, the robot arm is a 4-DOF (Degrees of Freedom) system featuring a 4-bar linkage mechanism. This design ensures that the end-effector consistently maintains a downward orientation during operation.
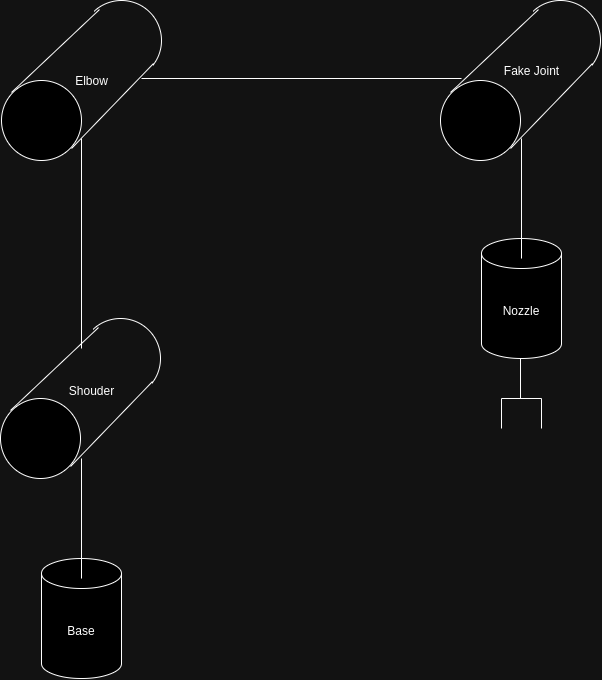
To accurately model the kinematics of the robot arm with its 4-bar linkage, I introduced a virtual joint (illustrated in the figure). This adjustment allowed for precise representation and computation of the robot’s motion dynamics.
The home configuration can be denoted as
\[M = \begin{bmatrix} 1 & 0 & 0 & L_3 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & L_1 + L_2 - L_4 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]And the ${\cal S}{list}$ and ${\cal B}{list}$ can be represented as
\[\begin{align*} S_{list} &= \begin{bmatrix} 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & L_3\\ 0 & L_1 & L_1 + L_2 & L_1 + L_2 & 0\\ 0 & 0 & 0 & -L_3 & 0 \end{bmatrix} \\ B_{list} &= \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ -1 & 0 & 0 & 0 & 1 \\ 0 & L_4 - L_2 & 0 & L_4 & 0 \\ 0 & 0 & 0 & 0 & 0\\ 0 & -L_3 & -L_3 & 0 & 0 \end{bmatrix} \\ \end{align*}\]Forward and Inverse Kinematics
After finishing modeling the robot, we could apply the equations described in book Modern Robotics for calculating the forward and inverse kinematics \(T_{sb}(\theta) = Me^{[{\cal B_1}]\theta_1}e^{[{\cal B_2}]\theta_2}e^{[{\cal B_3}]\theta_3}e^{[{\cal B_4}]\theta_4}e^{[{\cal B_5}]\theta_5}\)
Result
The assembled tangram puzzle is displayed in the figure below, demonstrating the robotic system’s ability to successfully complete a complex task. This result highlights the effectiveness of the system’s integration of advanced algorithms for sensing, planning, and manipulation in achieving precise assembly of the puzzle.
Future Work
There are some components in the project that requires improvements.
- Robot Control: Due to the hardware limitation, the robot actuators are not precise enough for accurately grasp all tangram pieces at all time, so in the future, I would implememt a close-loop robot control loop to use the apriltag mounted in the robot arm as feedback to
References:
-
Fernanda Miyuki Yamada, Harlen Costa Batagelo, João Paulo Gois, and H. Takahashi, “Generative approaches for solving tangram puzzles,” Discover Artificial Intelligence, vol. 4, no. 1, Feb. 2024, doi: https://doi.org/10.1007/s44163-024-00107-6.
-
K. M. Lynch and F. C. Park, Modern robotics : mechanics, planning, and control. Cambridge: University Press, 2017.
